이번 글에서는 광속 불변 조건에서 두 개의 관성좌표계에서의 시간과 공간의 변화가 어떻게 나타나는지 알아보겠습니다.
1. 로렌츠변환
앞선 글에서 빛의 속도가 불변할 때 두 관성좌표계의 시간과 공간의 값이 아래 식과 같이 뒤얽히는 것을 확인했습니다.

이 식의 갈릴레이 변환은 아래와 같습니다.

※ 갈릴레이 변환(Galilean transformation) : 2개의 관성좌표계가 서로 일정한 속도 v로 운동하고 있을 때, 좌표계간의 변환으로 고전역학 하에서의 변환식입니다.
하지만 광속불변 조건에서 이 식은 모순이 발생합니다. 광속불변을 만족하기 위해서는 아래와 같은 로렌츠 변환식을 이용해야 합니다.


2. 핵분열은 무엇인가요?
핵분열은 원자의 원자핵이 두 개 이상의 다른 원자핵으로 쪼개지는 현상입니다. 그리고 이때의 질량 차이만큼 에너지가 방출됩니다. 방출되는 에너지의 양은 아래의 유명한 식으로 계산할 수 있습니다.
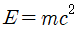
이 식은 아인슈타인이 1905년 특수상대성이론 논문에서 발표하였습니다. 질량과 에너지가 등가관계가 있다는 의미입니다. 핵분열이 가장 대표적인 예시입니다. 원자핵이 쪼개지는 과정에서 질량 결손이 발생하고, 그 질량만큼 위 식으로 계산된 에너지가 방출되는 현상입니다.
3. 근본적인 제한속도
두 관성좌표계의 이동속도가 V, V’이라고 가정했을 때, 고전역학에서 상대속도 v=V-V’이 됩니다. 특수상대성이론에서 로렌츠 변환을 이용하면 아래와 같습니다.

두 관성좌표계의 속도의 합은 그 개별의 속도가 광속보다 빠르지 않은 이상 광속을 넘어설 수 없습니다. 광속이 곧 근본적인 제한속도가 되는 것입니다.
4. 시간팽창과 길이수축
등속직선운동을 하는 관성좌표계(이때 이 좌표계의 시간은 t)를 관측하고 있는 정지한 관성좌표계(t’)를 가정하였을 때, 민코프스키 시공간에 대해 아래와 같습니다.

※ 민코프스키 시공간 : 특수 상대성이론을 잘 나타내는 시공간의 수학적 모델입니다.
이 식을 계산하여 풀어쓰면

이므로
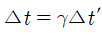
입니다. 이는 곧 운동하는 좌표계의 속력에 따라 γ(감마)의 값이 변하여 움직이는 좌표계에서 시간이 팽창(γ≥1)함을 알 수 있습니다. 반대로, 로렌츠 변환식을 이용하여 공간 성분에 대해 계산하면

이므로 관측되는 길이는 정지 상태에서의 길이에 비해 작아지며 길이가 수축함을 알 수 있습니다. 즉, 속도에 따라 시간이 팽창하고 길이가 수축하는 것입니다.
▼ 상대성이론 공부하기
상대성이론(1) - 아인슈타인 중력장 방정식, FLRW 계량, 텐서
상대성이론(2) - 맥스웰방정식, 광속불변, 시간과 공간의 뒤얽힘
상대성이론(3) - 로렌츠변환, 핵분열, 시간팽창과 길이수축
'학습 > 공학' 카테고리의 다른 글
| 상대성이론(4) - 쌍둥이모순, 도플러효과, 중력장 방정식에서 만유인력 (0) | 2022.07.27 |
|---|---|
| 4차산업혁명이 가져올 20년 후 미래와 문제점 (0) | 2022.07.26 |
| 상대성이론(2) - 맥스웰방정식, 광속불변, 시간과 공간의 뒤얽힘 (1) | 2022.07.24 |
| 상대성이론(1) - 아인슈타인 중력장 방정식, FLRW 계량, 텐서 (0) | 2022.07.23 |
| [제어공학] 기본신호, 연속시스템, 디지털 신호 등 신호와 시스템 개념정리 (0) | 2021.11.12 |
댓글