2차 제에시스템의 시간응답 특성에 대해서 알아보았다. 이번에는 근궤적법을 활용하여 해당 시스템의 특성방정식 근궤적을 그려보자.
이전글 - [전기공학] 제어공학 레포트(2) 제어시스템의 설계 - 2차 제어시스템의 시간응답 특성
https://gaesung.tistory.com/40
[전기공학] 제어공학 레포트(2) 제어시스템의 설계 - 2차 제어시스템의 시간응답 특성
이전 글에서는 위 제어시스템의 전달함수를 계산하고 Routh-Hurwitz 판별법을 사용하여 안정도를 판별하였다. 이번에는 해당 시스템의 시간응답 특성이 어떠한지 알아보자. 이전글 - [전기공학] 제
gaesung.tistory.com

1. 실수축과 만나는 점
위 시스템에서의 이득값을 K라고 하였을 떄의 이 제어시스템의 근궤적을 그려보자. 이 때, 특성방정식은 아래와 같다.

개루프 전달함수의 영점은 존재하지 않는다. 극점은 -1. -3. -10 으로 극점수가 3개다. 따라서 근궤적의 분기수 또한 3개가 된다. 따라서 실수축 위에 근궤적이 존재하는 부분은 아래와 같다.

극점이 3개인데 영점은 0개이므로 3개의 무한원점이 존재한다. 그리고 그 점근선을 구하면,


위와 같다. 점근선은 실수축의 -14/3 점에서 각각 60도, 180도, 300도 방향을 향하게 된다. 다음으로 근의 궤적이 실수축과 만나는 점을 구하면,

이고, 이를 정리하면 다음과 같다.

해를 구하면 근궤적의 접점을 알 수 있다.

이 중에서 -7.395는 근궤적의 실수축 위 존재 범위와 맞지 않는다. 위에서 근궤적 범위 식을 다시 보자. -1과 -3 사이거나 -10 이하인 값이어야 한다. 따라서 실수축과 만나는 점(실수축을 이탈하는 점)은 s=-1.938 이다.
2. 근궤적 그리기
허수축과 만나는 점은 Routh 표를 통해 구할 수 있다. 이득값이 K일 때의 Routh 표를 구하면 아래와 같다.

표에서 임계안정을 만족하는 K의 값은 572 다. K=572일 때의 특성방정식은 아래와 같다.
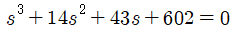
위 특성방정식을 인수분해 해서 근의 값을 구하면,

자, 이제 주어진 조건으로 근궤적을 그리면 아래 모습과 같다.

근궤적을 그리는데 사용된 조건을 다시 정리해보자.
1) 특성방정식의 근

2) 근궤적의 범위

3) 근궤적의 접점

4) 점근선의 접점과 각도


모두 근궤적 그림에 잘 표현되어 있음을 확인할 수 있다.
이득값이 K일 때의 근궤적과 조건들을 산출하였으니 다음 글에서는 백분율 오버슈트를 20%로 지정했을 때의 이득값 K가 몇이어야 하는지를 계산해보도록 하자.
다음글 - [전기공학] 제어공학 레포트(4) 제어시스템의 설계 - 이득값(K값) 계산, 적분제어기를 통한 정상상태오차 조정
https://gaesung.tistory.com/43
[전기공학] 제어공학 레포트(4) 제어시스템의 설계 - 이득값(K값) 계산, 적분제어기를 통한 정상상
이전글 - [전기공학] 제어공학 레포트(3) 제어시스템의 설계 - 특성방정식의 근궤적 그리기, 근궤적법 https://gaesung.tistory.com/41 [전기공학] 제어공학 레포트(3) 제어시스템의 설계 - 특성방정
gaesung.tistory.com
'학습 > 공학' 카테고리의 다른 글
| 에너지시스템(1) - 에너지의 역사와 발전과정, 경제와의 관계, 에너지 단위 (0) | 2021.08.14 |
|---|---|
| [전기공학] 제어공학 레포트(4) 제어시스템의 설계 - 이득값(K값) 계산, 적분제어기를 통한 정상상태오차 조정 (0) | 2021.08.05 |
| [전기공학] 제어공학 레포트(2) 제어시스템의 설계 - 2차 제어시스템의 시간응답 특성 (0) | 2021.08.01 |
| [전기공학] 제어공학 레포트(1) 제어시스템의 설계 - 전달함수와 Routh-Hurwitz 판별법 (0) | 2021.07.26 |
| [전기공학] 전기기기(4) - 직류발전기, 분권 발전기의 운전 특성 (0) | 2021.07.24 |
댓글