교류회로에서의 유도기전력과 정현파의 평균값, 실효값 공식유도 계산
1. 교류회로에서의 유도기전력

위 발전기의 원리를 나타낸 그림을 봅시다. N-S극의 자석으로 표현된 일정한 자기장 내에서 코일을 회전을 시킵니다. 이때 페러데이의 전자유도법칙에 의해 코일에는 유도기전력이 발생하게 됩니다.
여기서 코일은 각속도 ω로 회전하는데 속도 v가 일정하다고 한다면 코일은 등속 원운동을 하게 됩니다. N극에서 S극 방향을 x축, 그에 수직하는 방향을 y축이라 하고, 원점을 기준으로 반지름을 r이라 하면 코일의 변위는 아래와 같습니다.
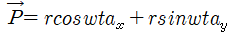
이때, 양변을 시간에 대하여 미분하여 코일의 속도를 계산해보죠. 코일의 속도와 자기장의 세기는 아래와 같은 식으로 계산할 수 있습니다.


이처럼 일정한 자기장 내에서 물체가 운동을 한다면, 그 물체를 기준으로 보았을 때 물체의 위치변화는 자기장의 변화와 같고, 그 방향은 서류 반대가 됩니다. 따라서 코일이 회전할 때 자기장의 변화는 다음과 같이 계산할 수 있습니다.

페러데이의 법칙에서 유도기전력 식에 위 식을 대입하면 아래와 같습니다.

자기장의 변화가 정현파(사인파)의 형태를 갖는 것처럼 유도기전력도 코일 회전에 따른 정현파의 형태가 됨을 알 수 있습니다. 계산식은 이러하고, 처음의 그림과 같은 형태의 발전기에서 유도되는 기전력을 구해봅시다.

도체가 2개의 권선으로 이뤄져 있으므로 N=2, A=l 임을 알 수 있습니다. 따라서 위 발전기에서 유도되는 기전력은 아래와 같습니다.
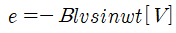
2. 정현파의 평균값과 실효값
□ 평균값
정현파의 파형은 1주기에 대해 양의 면적과 음의 면적의 합이 같습니다. 만약 1주기 전체에 대해 함수를 적분하여 평균값을 구한다면 그 값은 0이 될 것입니다. 따라서 정현파의 평균값은 부호를 고려하지 않고 파형을 적분한 반주기 평균값을 사용합니다. 이를 식으로 나타내면,
아래 정현파 함수에 대하여

1주기에 대한 평균치는 아래와 같습니다.

반주기 평균치는 아래와 같습니다.
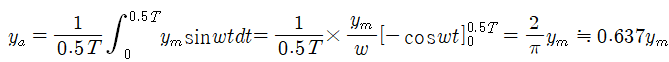
□ 실효값
전력과 전류 혹은 전압의 관계에서

위와 같은 관계가 성립합니다. 교류전력이 일을 할 때는 사인파형에 대한 평균치가 아닌 사인파를 제곱한 값의 평균값에 대한 제곱근 값, 즉 실효값을 구해야 합니다. 임의의 부하 R과 연결된 교류전원 v(t)가 있을 때, 흐르는 전류 i(t)의 실효값을 구해봅시다.
교류 전류를 식으로 표현하면 아래와 같습니다.

이를 제곱하면 이렇게 되겠죠.

여기서 sin 함수의 제곱에 대한 삼각함수 공식을 사용합니다. 삼각함수의 반각공식이라고 고등학교 수학과정에서 외우는 공식 중 하나죠.

이를 대입해서 식을 정리하면,

위와 같이 쓸 수 있습니다. 여기서 cos2ωt와 i(t)의 주기가 2배 차이나므로 i(t)의 반주기의 시간에 대해 cos2ωt는 1주기가 됩니다. 정현파의 1주기 평균값은 0이므로 cos2ωt의 평균값은 0도 됩니다. 반주기에 대해 전류의 제곱은 아래와 같습니다.
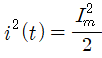
마지막으로 제곱근 값을 구하면,
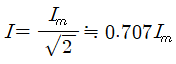
입니다. 사인파에서 실효값은 최대값을 루트 2로 나눈 값이라는 것을 알 수 있네요. 반대로 실효값을 알고 있다면 루트 2를 곱해서 최대값을 계산할 수 있습니다.